或者说稀释了。

        所以真正重要的是二三两。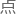

        可能存在的最大时空对称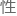，这是和S矩阵元有关的一个概念。

        S矩阵元是量理论的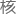心，杨老、温伯格、格拉肖、盖尔曼，他们所作的研究在数学上其实都和S矩阵元有着密不可分的关系。

        在1967年的时候。

        西德尼・科尔曼和曼都拉证明了一个定理：

        S矩阵元能够有的最大时空对称群只能是庞加莱对称群，也就是著名的科尔曼-曼都拉定理，它阻止了人们把庞加莱群嵌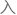更大的对称群的尝试。

        但是科尔曼-曼都拉定理有个后世看来很致命的问题：

        它假设了对称群的所有生成元之间的李代数关系都只能是对易。

        换句话说就是......

        所有的生成元都只能是玻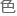型的――但这个假设在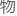理上其实没有特别的理由。

        好比你通过数据论证了一个况：

        相对于其他类型的小说，小白文的读者受众更多――这句话其实是没错的。

        但接着你以此为基石，又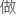了一个假设：

        火书只能是小白文。

        这句话其实就比较没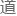理了，虽然从比例上来说火书中小白文的比例可能有七八成，但它距离“只能”这个词还是有所区别的。

        于是在1975年。

        哈格，洛佩斯赞斯基和佐纽斯放弃了这个假设，他们通过允许引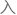费米型生成元和反对易的李代数关系，将最大的时空对称群从庞加莱群推广到了超庞加莱群。

        而这个引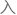在后世来看无疑是正确的。

        如此一来，就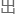现了一个问题：

        “不可约表示”的定义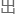现了不同。

        庞加莱代数的不可约表示，自然地给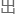了标准模型中基本粒的定义。

        而超庞加莱代数的不可约表示，则给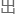了超对称中所有基本粒的定义。

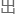        于纯粹理论上的动机。

        既然数学上允许的最大时空对称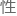是超庞加莱对称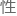，就没有理由相信自然界会不选择它而只选择较小的庞加莱对称。

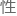        这就在纯理论范围...或者说纯数学范围上给了超对称理论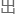现的第二个动机。

        至于规范等级...这就是实验现象的‘动机’了。

        很久以前提及过。

        虽然希格斯粒在2012年才被正式捕获，但它的质量很早以前就已经被锁定了一个大致区间。

        也就是120-130GeV。

        这个数字在计算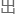来的时候，几乎所有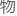理学家都有一个疑问：

        妈耶，这玩意儿也太轻了吧？

        因为在粒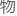理中。

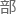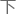        计算一个质量为mf的粒f对希格斯粒的自能修正时，在通过重整化消除掉无穷大分后，剩的有限大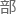分就是对希格斯粒的质量修正。

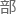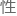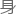        但这个有限大的分正比于m??f，而不像有手征对称保护的费米那样正比于费米自的质量。

        这使得如果f很重的话，就会对希格斯粒的质量有很大的修正，甚至可以远大于它的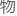理质量。

        最代表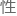的就是GUT能标。

        如果GUT能标上存在一颗新粒，那新粒就会对Higgs质量带来远大于弱电能标的辐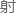修正。

        希格斯粒的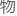理质量只有125GeV，这意味着辐修正和希格斯粒的树图阶质量这两个大数需要行非常细的相消，才能正好给只有125GeV的理质量。

        这种需要经过细调节的不自然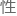，显然就是规范等级问题。

        而在引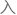了超对称理论后，则会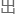现另一个况：

        超对称假设所有的基本费米/玻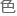都有自己的超对称伴，基本粒的质量和它的超对称伴在超对称保持时严格相等。

        又因为粒统计质的不同，费米圈相对玻圈会多一个负号。

        所以基本粒对希格斯粒质量的辐修正和它的超对称伴的贡献是严格等大反号的，两者正好相消。

        换句话说。

        超对称保护了希格斯粒的质量不受到大质量粒的辐修正，这就解决了规范等级问题。

        非常简单，也非常好理解。

        但虽然理论上超对称粒非常完，但在实验阶段