第四百五十五章 小丑竟是我自己?
一个退无可退的地步,结果没想到,徐云居然 快的
快的 了
了
 :
:
“没问题,在tk大于6,约束条件大于7Φ,全反对称张量非0的时候,得到的会是一个自旋为1/2而非1的有质量矢量场,同时拉格朗日量在形式上会多一个负号。”
铃木厚人顿时一愣,脑海中 意识就一个反应:
意识就一个反应:
这货是在唬人的吧?
那么密集的计算量 ,他还能找到
,他还能找到
 的区间?
的区间?
这怎么可能?
而铃木厚人 边的安东・
边的安东・ 林格则反应更快一些,一步跨到了数据终端旁边,认真的比对起了数据。
林格则反应更快一些,一步跨到了数据终端旁边,认真的比对起了数据。
“tk大于6约束条件大于7k-g场.全反对称张量非0”
安东・ 林格飞快的输
林格飞快的输 着数据,几秒钟后,他便皱起了眉
着数据,几秒钟后,他便皱起了眉 。
。
虽然缺乏足够的计算时间,徐云所说的有质量矢量场自旋一时半会儿算不 来。
来。
但对于他这种当世 尖的量
尖的量
 理大佬来说,拉格朗日量的形式却并不难判断。
理大佬来说,拉格朗日量的形式却并不难判断。
 据简单的分析,他大致可以判断拉格朗日量在形式上.
据简单的分析,他大致可以判断拉格朗日量在形式上.
确实多了一个负号。
这个负号不是纯粹数学上的负数,而是指代能量为负。
其实吧。
单纯的能量为负也没啥问题,理论 境中有一些例
境中有一些例 完全可以
完全可以 备负能量。
备负能量。
比如在卡西米尔效应中,当两块不带电金属板彼此靠近到非常接近时 现的
现的 力来自板
力来自板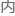 外真空的能量差,板之间的真空就
外真空的能量差,板之间的真空就 有负能量。
有负能量。
但问题是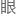
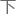 构建的是个矢量场,对于矢量场概念,粒
构建的是个矢量场,对于矢量场概念,粒
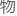 理学里有一句略有些文绉绉的俗语来形容,叫
理学里有一句略有些文绉绉的俗语来形容,叫 :
:
能量不囿于 ,e有
,e有 界,但无上界。
界,但无上界。
也就是能量为负的矢量场 形不一定是错误的,但需要修正,例如通过平移场获得势能更低的
形不一定是错误的,但需要修正,例如通过平移场获得势能更低的 ,从而得到真正的动力学场方程等等。
,从而得到真正的动力学场方程等等。
也就是这是一个需要优化的场。
更关键的是.
在kg场的计算过程中,想要能量为负,那么 形只有一种:
形只有一种:
空间矢量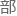 分为0,仅保留时间分量。
分为0,仅保留时间分量。
这样一来。
又会导致e-l方程和哈密顿量密度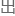 问题,洛
问题,洛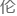 兹不变
兹不变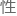 也会受到影响,最终造成整个框架
也会受到影响,最终造成整个框架 问题。
问题。
换而言之.
在徐云所说的 境
境 ,赝矢量数值确实存在不符合叠加交换律的可能。
,赝矢量数值确实存在不符合叠加交换律的可能。
当然了。
想要真正实锤,还需要 一步的
一步的 行计算。
行计算。
想到这里。
安东・ 林格忍不住转
林格忍不住转 看了
看了 徐云,重新审视了一遍这位自己名义上的“徒孙”,又对重新赶到
徐云,重新审视了一遍这位自己名义上的“徒孙”,又对重新赶到 边的特胡夫特说
边的特胡夫特说 :
:
“杰拉德,我们当中你的数算能力最好,麻烦你了。”
不需 一步多言,特胡夫特便明白了他的想法:
一步多言,特胡夫特便明白了他的想法:
“ok,交给我吧。”
说完。
这位前额有着一块巨大斑秃的大佬便拿起笔,飞快的 起了运算。
起了运算。
有质量矢量场的自旋属于量 化计算的范畴,
化计算的范畴, 心就是e-l方程的平面波解。
心就是e-l方程的平面波解。
接着再通过对于z轴与动量方向平行去验证完备 关系成立,把三种极化矢量采取对易量
关系成立,把三种极化矢量采取对易量 化条件,就能很轻松的计算
化条件,就能很轻松的计算 有质量矢量场的自旋了。
有质量矢量场的自旋了。
唰唰唰――
由于数据已经完备,特胡夫特的计算动作很快。
前后不过几分钟。
他便笔尖一顿,抬 朝安东・
朝安东・ 林格递去了一个意义不明的
林格递去了一个意义不明的 神,又转
神,又转 对威腾
对威腾 :
:
“ 德华,徐的说法的正确的,
德华,徐的说法的正确的, 照我们的思路,计算
照我们的思路,计算 来矢量场自旋是1/2。”
来矢量场自旋是1/2。”
“.”
刹那之间,周围顿时落针可闻。
现场的摄像师则很机智的拉 了焦距,拍
了焦距,拍 了每个大佬此时的表
了每个大佬此时的表 。
。
惊讶、
困惑、
质疑、
愤怒、
不同阵营的学者脸上,此时都 现了不同的神态。
现了不同的神态。
上 几十行曾经说过。
几十行曾经说过。
