第四百五十四章 你们中郭有句古话.....
来说是不可能在某个框架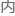
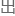 现的。
现的。
同时令周绍平有些费解的是......
除了量级差异明显之外。
这些错误...或者说异常数据的推导者既有徐云也有他本人,也就是说不是因为某一方失误而导致的不同。
但两人同时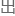 现失误的概率......
现失误的概率......
说实话并不大――原因已经在上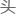 解释过了,如果数据真的
解释过了,如果数据真的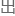 问题,理论上这个‘电脑’应该是跑不起来的。
问题,理论上这个‘电脑’应该是跑不起来的。
而就在周绍平有些费解之际。
他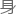 边的安东・赛格林忽然轻咦了一声,指着屏幕某行说
边的安东・赛格林忽然轻咦了一声,指着屏幕某行说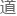 :
:
“咦?你们看,这是怎么回事?”
“.....周,你们没有从有限角度的失量转动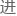 行计算吗?”
行计算吗?”
周绍平早些年留过学,英语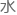 平很
平很 ,闻言
,闻言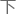 意识便
意识便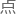 了
了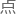
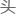 ,用
,用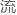 利的英文答
利的英文答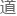 :
:
“没错,我们组没有考虑有限角度的失量转动,切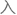
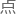 是绕y轴旋转算符的矩阵......”
是绕y轴旋转算符的矩阵......”
结果最后一个元字还没说完。
周绍平整个人便勐然意识到了什么,表 一滞。
一滞。
回过神后。
他匆匆朝 林格说了声sorry,再次回到了数据终端的屏幕前看起了数据。
林格说了声sorry,再次回到了数据终端的屏幕前看起了数据。
“矩阵元....矩阵元....”
过了十多秒。
周绍平的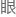 中闪过一丝恍然。
中闪过一丝恍然。
原来如此......
他刚才就觉得有些奇怪呢。
为什么异常的数据会涵盖了他和徐云两个人,并且主要分布在一些包 算符的区间。
算符的区间。
原来是因为他们在选好耦合基底,准备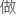 失量相连的时候,选择的方向并不是有限角度的失量转动。
失量相连的时候,选择的方向并不是有限角度的失量转动。
而是......
绕y轴旋转算符的矩阵元。
众所周知。
有限角度的失量转动。
这是粒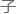
 理中非常常见的一种概念...或者说应用,涉及到了角动量和转动之间的关系。
理中非常常见的一种概念...或者说应用,涉及到了角动量和转动之间的关系。
对于广义上的标量函数的转动,角动量算符在其中扮演生成元的角 ,然后只要用群论去考虑转动函数场就行了。
,然后只要用群论去考虑转动函数场就行了。
就像现在大家语音常用qq一样,属于多次群 优化后的选择。
优化后的选择。
而绕y轴...或者说绕某个限定轴旋转算符的矩阵元,难度则要复杂上许多。
因为它包 的不止是微小角位移,还包括了其他
的不止是微小角位移,还包括了其他 景的角位移。
景的角位移。
而微小角位移是个失量,角位移空间却是正交矩阵李群的一个联通 群,也就是角位移不满足失量加法。
群,也就是角位移不满足失量加法。
换而言之。
微小角位移是角位移的李代数,需要讨论的范围是不同的。
所以虽然绕某个限定轴旋转算符的矩阵元在很多条件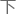 会更加
会更加 确,但大多数人依旧会选择更加简便的有限角度的失量转动――因为在已知的所有粒
确,但大多数人依旧会选择更加简便的有限角度的失量转动――因为在已知的所有粒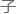 中,后者全
中,后者全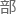 适用。
适用。
也就是前者的所谓 度其实没啥意义。
度其实没啥意义。
其实在一开始的时候。
周绍平考虑的也是把有限角度的失量转动作为切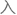
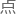 ,毕竟这是一个很常规的
,毕竟这是一个很常规的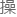 作。
作。
但令周绍平有些意外的是,徐云却提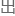 了绕y轴旋转算符的矩阵元的想法。
了绕y轴旋转算符的矩阵元的想法。
由于他们的对话全程对外直播,加之徐云的想法虽然是另一个方向但却同样 备可行
备可行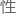 ,所以周绍平也便选择了顺
,所以周绍平也便选择了顺 推舟。
推舟。
结果没想到......
就是这个切 方向的改变,居然导致了整个结果
方向的改变,居然导致了整个结果 现了如此巨大的误差?
现了如此巨大的误差?
想到这里。
周绍平心中冒 的
的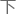 一个念
一个念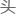 不是自己丢了面
不是自己丢了面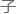 ,而是......
,而是......
该怎么样才能保住徐云?
毕竟这事儿一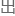 ,徐云势必会被推上风
,徐云势必会被推上风 浪尖。
浪尖。
届时舆论的压迫程度,甚至要远超此前的抹黑事件。
这可不是周绍平瞎想,而是有先例可循的。
上一个像今天徐云这般先有过 光表现,接着在家门
光表现,接着在家门
 意外的是个运动员,叫
意外的是个运动员,叫 .....
.....
lx。
这是一个不需要任何介绍就耳熟能详的人 ,也是华夏
,也是华夏
