第四百一十章 建国后高能物理最重要的成果...诞生!(中)
这里的“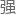 ”对应
”对应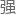
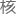 力,cp则是指chargeparity,也就是电荷-宇称。
力,cp则是指chargeparity,也就是电荷-宇称。
对 等
等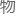 理比较了解的同学应该知
理比较了解的同学应该知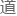 。
。
 等
等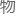 理的很多问题在不同
理的很多问题在不同 况
况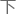 往往会有着不同的解,而这些解有个统一的称呼:
往往会有着不同的解,而这些解有个统一的称呼:
度规。
最有名的就是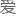 因斯坦场方程组。
因斯坦场方程组。
目前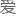 因斯坦场方程组的度规有好几个,比如克尔度规、史瓦西度规等等......
因斯坦场方程组的度规有好几个,比如克尔度规、史瓦西度规等等......
同时,这些度规还会对应某个模型。
例如克尔度规对应的就是克尔黑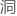 。
。
哥德尔度规对应的就是哥德尔宇宙等等......
顺便一提。
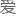 因斯坦方程还有一个特殊的时空度规,叫
因斯坦方程还有一个特殊的时空度规,叫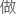 阿库别瑞度规。
阿库别瑞度规。
也就是科幻片经常提到的“泡泡曲率引擎”。
这玩意儿很离谱的一 是,它的概念先
是,它的概念先 现于科幻片,然后阿库别瑞才在1994年得
现于科幻片,然后阿库别瑞才在1994年得 了这个解。
了这个解。
也就是幻想在前,理论在后。
究竟是科学引导了科幻,还是科幻启发了科学?
好了。
话题回归原 。
。
正如上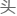 所说的那些度规一般。
所说的那些度规一般。
peccei-quinn度规,也是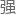 pc问题的一个特定解。
pc问题的一个特定解。
这是peccei以及quinn在70年代提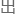 来的peccei-quinn机制,helenquinn也是最有希望拿到
来的peccei-quinn机制,helenquinn也是最有希望拿到 能
能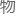 理诺贝尔奖的女
理诺贝尔奖的女 理学家。
理学家。
它在某个能级 可以构建
可以构建 一个暗
一个暗 质的检验框架,并且超对称伴
质的检验框架,并且超对称伴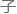 也符合4685Λ超
也符合4685Λ超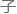 的特
的特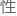 。
。
同时它能够调整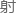 散角,通过最靠谱的光程差来排除误差。
散角,通过最靠谱的光程差来排除误差。
当然了。
peccei-quinn度规同样也有一些技术上的难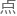 ,
,
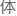 是否可行还要
是否可行还要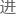 行更详细的讨论。
行更详细的讨论。
这些院士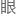
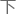 要
要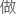 的,还是先
的,还是先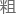 略筛选
略筛选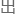 一些相对可行的方案,然后再
一些相对可行的方案,然后再 行逐一甄别。
行逐一甄别。
因此很快。
众多院士又继续开始了新一轮的 脑风暴:
脑风暴:
“除了peccei-quinn度规,我觉得让带电粒 划过tpc也是个不错的想法嘛......”
划过tpc也是个不错的想法嘛......”
“要不和神冈那样用重 中的氘去探测中微
中的氘去探测中微 ?小季这里的重
?小季这里的重 应该有不少。”
应该有不少。”
“电离加声 如何?”
如何?”
“我们之前搞 达的那个cq机制我认为可行.......”
达的那个cq机制我认为可行.......”
.........
一个多小时后。
五个候选方案被摆到了众人面前:
peccei-quinn度规。
上9千克的ge靶材。
检测暗 质对原
质对原 钟的影响。
钟的影响。
 一步捕捉暗
一步捕捉暗 质的次级粒
质的次级粒 。
。
以及.....
允许误差存在,通过多论实测曲线 行拟合分析。
行拟合分析。
接着很快。
次级粒 的方案首先被排除了。
的方案首先被排除了。
次级粒 属于间接探测的范畴,它的原理很简单:
属于间接探测的范畴,它的原理很简单:
是让暗 质粒
质粒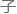 的次级粒
的次级粒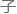 与探测
与探测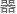 发生相互作用,从而间接获得暗
发生相互作用,从而间接获得暗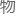 质粒
质粒 的信息。
的信息。
就好比妈妈是暗 质粒
质粒 ,孩
,孩 是暗
是暗 质粒
质粒 衰变产生的次级粒
衰变产生的次级粒 。
。
由 针第一定律可知,孩
针第一定律可知,孩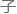 是妈妈省的。
是妈妈省的。
接着呢。
科学家们用相机给孩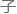 们拍照,通过孩
们拍照,通过孩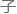 们的长相倒推
们的长相倒推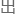 妈妈的长相。
妈妈的长相。
这种 法在常规研究中不失为一种思路,难度也相对低
法在常规研究中不失为一种思路,难度也相对低 ,而且还非常有意思。
,而且还非常有意思。
但在
 这个场合,显然不太合适。
这个场合,显然不太合适。
接着很快。
二、三两个方案也被排除了。
这两种方案同样很难降低放
 背景的影响,起不到多少实际的作用。
背景的影响,起不到多少实际的作用。
因此摆在众人面前的,只剩 了两个方案:
了两个方案:
用peccei-quinn度规模型复验。
或者允许误差存在,通过多轮实测曲线 行拟合分析。
行拟合分析。
然后......
众人的意见便产生了很严重的分歧。
在这27位院士中。
除了王老、张老和侯星远没有表态外,支持两种方案的院士各占一半。
“各位,我还是 持peccei-quinn度规。”
持peccei-quinn度规。”
周绍平先是拿起桌上的茶 抿了一
抿了一 ,又环视了周围
,又环视了周围