第三百七十五章 好久不见,麦克斯韦
片刻之后。
????????最上方的区域缓缓发 了金光,一个名字悄然在空气中浮现∶
了金光,一个名字悄然在空气中浮现∶
????????jasclerkmaxell。
????????过了一会儿。
????????一位面 略显苍白、
略显苍白、 形瘦弱、蓄着一缕大胡
形瘦弱、蓄着一缕大胡 、腰间别着一把斧
、腰间别着一把斧 的中年人虚影从中走
的中年人虚影从中走 。
。
????????只见他凝视了徐云两秒钟,接着化作金光飞 了徐云
了徐云
 。
。
????????与此同时。
????????徐云的 中骤然一清,发现自己的思绪再次开阔了起来。
中骤然一清,发现自己的思绪再次开阔了起来。
????????过了几秒钟。
????????他看着自己的手掌,面带 慨的叹息一声∶
慨的叹息一声∶
????????“好久不见了,小麦。”
????????随后他用力甩了甩 ,飞快的将思绪聚焦到了面前的
,飞快的将思绪聚焦到了面前的 斯手稿上。
斯手稿上。
????????稍作犹豫,便提笔飞快的写了起来:
????????“解”
????????“引理:若n&a;gt;1,a~n-1是素数,则a=2,n是素数。”
????????“......当n&a;gt;1时,若a&a;gt;2,则a^n-1=(a-1)(a^n-1 a^n-2 a^n-3 ... a 1)......“
????????“可知a~n-1是合数,所以a=2。”
????????“若n是合数,n=xy,x&a;gt;1,y&a;gt;1,于是有2~xy-1=(2~x-1)(2~x(y-1) 2~x(y-2) 2~x(y-3
????????) ... 1)”
????????“由此可知2~n-1是合数。”
????????写完这些。
????????徐云微微顿了顿,将 斯的手稿挪到了手边。
斯的手稿挪到了手边。
????????“由不存在奇完全数可知,设正整数n有素因 分解n=p~(a1/1)p~(a2/2)p~(a3/3)....p(as/s)。”
分解n=p~(a1/1)p~(a2/2)p~(a3/3)....p(as/s)。”
????????“由于因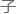 和函数σ是乘
和函数σ是乘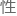 函数,那么可得∶”
函数,那么可得∶”
????????“σ(n)=ip^(a1 1/1)-1)/kp1-1|・ip~(a2 2/1)-1】/kp2-1}・|p~(a3 3/1)-1]/1p3-11............・ip^(as s/1)-1}/kps-1}=sttj1・ip^(aj j/1)-1)-10-1]......”
????????………
????????就这样。
????????徐云洋洋洒落的在a4纸上飞快书写,时间也一分一秒的缓缓 逝。
逝。
????????塔形数.....
????????排中律......
????????单未知数…...
????????徐云仿佛回到了1850年的剑桥大学,当时他也是这样坐在书桌边和小麦讨论着各种问题。
????????只是当初徐云是老师,小麦是学生。
????????而这一次……
????????徐云变成了学生,小麦则成为了老师。
????????一个小时后。
????????徐云的笔尖微微一顿,写 了最后一行字:
了最后一行字:
????????“综上所述,故....存在无穷多个梅森素数。”
????????与此同时。
????????他的
 莫名一震。
莫名一震。
????????原本急速转动的思绪,骤然停止了 来。
来。
????????过了几秒钟。
????????徐云轻轻呼 了
了 绵长的气息,带着
绵长的气息,带着 慨,带着追忆。
慨,带着追忆。
????????“多谢你了,麦克斯韦.....”
????????・・・・・
????????注∶
????????吃坏肚 了,今天少
了,今天少 ,明天要是还不好可能要去挂
,明天要是还不好可能要去挂 。
。
/78/78112/31487792.html